نظرة بسيطة لخوارزميات الترتيب - Les algorithmes de tri
السلام عليكم ورحمة الله وبركاته
سنتحدث في هذا الموضوع عن ماهية خوارزميات الترتيب المعتمدة في البرمجة وفي الإعلام الآلي بصفة عامة، وعن دور هاته الخوارزميات وأهميتها منذ ظهور الإعلام الآلي وخاصة دورها في البرمجة ومدى تطورها عبر الأزمنة.
لقد شغل مشكل ترتيب البيانات عقول الكثير من المبرمجين والرياضيين خاصة منذ ظهور الإعلام الآلي في بداية القرن العشرين، فكان كل عالم يبحث عن أفضل طريقة لترتيب البيانات المخزنة في مكان ما، أو البيانات التي تم إدخالها من طرف المستخدم في جهاز ما كالكمبيوتر أو جهاز آخر.
ما هي خوارزمية الترتيب في مجال الإعلام الآلي ؟
يقصد بالترتيب هنا هو تنظيم مجموعة من البيانات موجودة في نوع من البنيات التي نعرفها في البرمجة مثل الجداول (Tableau) أو القوائم المترابطة (Listes chainnées) أو أي نوع آخر من البنيات أو الهياكل الأخرى التي نراها موجودة في البرمجة، ويكون تنظيم هذه المعلومات وفق علاقة ترتيب معينة (Relation d'ordire) في مجموعة تقبل ترتيباً كلياً (Ordre total)، ربما هذا التعريف غامض لكن بوضع مثال يمكن توضيحه بعض الشيء :
مثلاً في مجموعة الأعداد الطبيعية N، يمكننا ترتيب معطيات موضوعة في جدول ما وفق علاقة الترتيب : أصغر >
2 | 10 | 0 | 2 | 1 | 5 | 3 |
يمكننا ترتيب الأرقام الموجودة في هذا الجدول وفق علاقة الترتيب التي نريدها، مثلاً العلاقة : أصغر > وبهذا يكون ترتيب هذه الأرقام تصاعدياً أو وفق علاقة الترتيب أكبر < وبهذا يكون ترتيب هذه الأرقام تنازلياً
إذا إخترنا العلاقة الأولى (أصغر >) فيمكننا القيام يدوياً بترتيب هذه الأعداد كما كنا نفعل في المدرسة الإبتدائية، فتصبح النتيجة كالتالي :
10 | 5 | 3 | 2 | 2 | 1 | 0 |
نلاحظ أنه في هذه الحالة الجدول متكون من سبعة أعداد أكبرها العدد 10، فلم يستغرق ترتيبها أكثر من 30 ثانية أو أقل وذلك لقلة الأعداد التي نرتبها لكن لو كان الجدول مكون من 1000 عدد وطلب منا ترتيبها فسيكون الأمر صعباً نوعاً ما وسيستغرق على الأقل ساعة كاملة في الترتيب والنسخ واللصق وإعادة الكتابة والحذف .. (حتى ولو كانت الأعداد في الجدول صغيرة مثلاً أكبرها العدد 10 كالمثال السابق)
إذا كان الجدول مكون من 5000 عدد وطلب منا ترتيبهاً، فهنا الأمر صعب جداً ولا يمكن القيام به يدوياً (إلا إذا أراد احد تخصيص يوم كامل لترتيب جدول بهذا الطول  )
)
فهنا لا يمكن القيام بالأمر يدوياً ويجب الإستعانة بآلة قابلة للبرمجة مثل الحاسوب أو سمارت فون أو أي آلة أخرى ونطبق إحدى خوارزميات الترتيب .
نواصل في مثالنا السابق وهو ترتيب جدول مكون من 7 أعداد أكبرها العدد 10. في حالة لو طلب منا ترتيب الجدول وفق العلاقة الثانية (أكبر <) فيمكننا القيام بذلك يدوياً لصغر طول الجدول، فتصبح النتيجة كالتالي :
0 | 1 | 2 | 2 | 3 | 5 | 10 |
الأمر سهل يدوياً ولم يستغرق أكثر من 30 ثانية لأن الجدول متكون من 7 أعداد فقط ^^
كان بإمكاننا إختيار علاقات ترتيب اخرى لنقوم بترتيب الجدول بالإعتماد عليها ( لكن في حالتنا هنا لا أرى مثال لعلاقة ترتيب أخرى، ربما الأمر ممكن لو كان الجدول مكون من ثنائيات (x,y) فيمكننا إختيار علاقة أخرى مثل علاقة الترتيب ~ التي نُعرفها كالتالي :
(x,y) ~ (x',y') <==> (x < x') أو (x = x' et y < y')
هذه العلاقة تسمح لنا بترتيب جدول مكون من ثنائيات (x,y) مثلا:
(2,0) | (0,2) | (6,1) | (2,2) | (10,2) | (1,4) | (4,3) |
عندئذ يمكننا ترتيب الجدول وفق هذه العلاقة والحصول على الجدول التالي :
(10,2) | (6,1) | (4,3) | (2,2) | (2,0) | (1,4) | (0,2) |
لماذا نحتاج إلى خوارزميات الترتيب ؟
لقد ذكرت في المثال السابق جدولاً مكوناً من 7 أعداد فقط حيث إستغرق ترتيبها 30 ثانية (ترتيباً تصاعدياً أو تنازلياً) ، لكن لو كان الجدول أطول من ذلك مثلاً مكون من 100 عدد فربما سيستغرق الامر أكثر من 30 ثانية لترتيبه وفق علاقة ترتيب معينة، كذلك الامر لو كان الجدول مكون من 1000 عدد ؟ 5000 عدد ؟ أو حتى 10000 عدد في بعض الحالات.
في البرمجة بصفة خاصة، المبرمج قد يصادفه أثناء برمجته لبرنامج تسيير أجور عملاء مؤسسة ما الرغبة في ترتيب قائمة هؤلاء العملاء وفق علاقة ترتيب معينة، مثلاً ترتيب قائمة العملاء ترتيباً أبجدياً (أي وفق اللقب والإسم) أو ترتيبهم من الأكبر سناً إلى الأصغر (ترتيب وفق تاريخ الإزدياد) أو ترتيبهم من الأكثر دخلاً إلى الأقل دخلاً (أي ترتيب وفق الدخل الشهري أو السنوي) ، فلو كان في المؤسسة 100 عامل فسيتطلب ترتيب قائمة هؤلاء العمال وفق علاقة ترتيب ذكرناها سابقاً إستعمال إحدى خوارزميات الترتيب التي سنرى بعضاً منها في هذا الموضوع.
هناك عدة أمثلة لإستعمالات خوارزميات الترتيب في البرمجة أو الإعلام الآلي بصفة عامة، فهاته الخوارزميات تعتبر من أساسيات البرمجة وعلى كل مبرمج أن يتقن إستعمال بعضها والتعامل معها وفق الحاجة (يجب حفظها إن تطلب الأمر lol ^^)
كيف أختار خوارزمية الترتيب التي تناسب برنامجي ؟
إختيار خوارزمية الترتيب المناسبة للبرنامج يتطلب أولاً دراسة للمشكل ومعرفة خصائصه ويقصد هنا بالمشكل المعطيات المراد ترتيبها وتنظيمها وفق علاقة ترتيب معينة، أي بمعنى آخر طبيعة المعطيات : هل هي أعداد ؟ جمل ؟ ثنائيات ؟ ..
وما هي البنية أو الهيكلة (Structure de données) التي تحتوى هاته المعطيات ؟ هل هي في جدول ؟ أو سلسلة مترابطة ؟ ذات إتجاه واحد أو إتجاهين ؟ .. إلخ من الاسئلة التي تسمح لنا بدراسة هذا المشكل وإختيار الخوارزمية المناسبة له.
خوارزميات الترتيب كثيرة وعديدة، فكما ذكرت سابقا فإن مشكل ترتيب البيانات مشكل مطروح منذ السابق وقد ساهم الكثير من العلماء الرياضيين والمبرمجين في إبتكار خوارزميات ترتيب جديدة أقوى من الخوارزميات السابقة وأفضل منها.
أقوى من حيث ماذا ؟ وأفضل من حيث ماذا ؟
يمكن تصنيف خوارزميات الترتيب وفق عدة عوامل : سنذكر عاملين مهمين في تصنيف هاته الخوارزميات هما السرعة والفضاء المستهلك (التعقيد الزمني والتعقيد الفضائي).
طبعاً قد نتسائل، لماذا يجب علينا الإهتمام بكل هاته التفاصيل (التعقيد الزمني والتعقيد الفضائي) ؟
المبرمج يبحث دائماً عن الحل الأفضل للمشاكل التي يواجهها أثناء برمجته لبرنامج ما سواء كانت مشاكل تتعلق بالترتيب، البحث أو الحسابات أو أي مشاكل أخرى قد تواجهه أثناء القيام ببرمجة برنامجه.. فلو أخذنا مشكل الترتيب فعليه أن يجد أفضل خوارزمية ترتيب تساعده على معالجة المعطيات التي لديه وتقوم بحل هذا المشكل في أقصر مدة زمنية وبأقل جهد ممكن. الآن نعيد صياغة سؤالنا : كيف يمكن الحكم على خوارزمية ترتيب أنها أفضل من خوارزمية أخرى ؟
السرعة والفضاء المستهلك، كلمتان مهمتان في التكنولوجيا الحديثة (وحتى القديمة منها) فلو سألنا أي شركة برمجيات بصفة خاصة أو تكنولوجيات بصفة عامة مثل Samsung, IBM, Intel .. عن ما يؤرق علمائها وما يشغلهم أكثر فسنجد الإجابة أنهم يبحثون عن التكنولوجيا السريعة على الإطلاق، التكنولوجيا التي تستغرق أقل مدة زمنية لتقوم بالدور المطلوب منها وتقوم بمعالجة ما يعطى إليها في أقصر زمن ممكن على الإطلاق !
فعند صناعة هاتف نقال، أو حاسوب، أو أي تكنولوجيا أخرى فالعامل الأول للحكم عليها هو سرعة هاته الآلة وكم تستغرق من زمن للقيام بالمهمة المطلوبة منها بأكمل وجه ؟ (دقيقتين ؟ ثانية ؟ كم جزء من ألف من ثانية ؟) فنجد في عالم المعالجات وحدة قياس سرعة المعالج MIPS: million instructions par seconde، مليون تعليمة خلال ثانية واحدة، كلما كان هذا الرقم أكبر كان المعالج أفضل وأحسن .
الإجابة الثانية ستكون أن أغلب الشركات تبحث عن التكنولوجيا التي تستهلك أقل ما يمكن من الموارد أي أن هذه الآلة تكون صغيرة الحجم ولا تشغل حجماً كبيراً، ولا تستهلك موارد كثيرة فكل شيء له ثمن ^^
فهناك فرق بين آلتان تقومان بنفس العمل وتعطيان نفس النتيجة لكن هناك من تستهلك موارد أكثر من الاخرى وبالتالي جهد وثمن أكبر من الآلة الأخرى.
وطبعاً عدم إستهلاك الآلة الكثير من الموارد يعني أنها لن تكون مرفقة بموارد إضافية تزيد في حجمها وفي ثمنها لأنه كما قلنا لكل شيء ثمن  (خاصة الـ Hardware فحتى البرغي له ثمنه الخاص)
(خاصة الـ Hardware فحتى البرغي له ثمنه الخاص)
حتى لا نخرج عن موضوع خوارزميات الترتيب، سنقوم بإسقاط ما تكلمنا عنه (السرعة والفضاء المستهلك) على موضوعنا وهي خوارزميات الترتيب التي سنراها فيما بعد إن شاء الله. يمكننا الحكم على خوارزمية أنها أفضل من الأخرى بمعيارين مهمين هما سرعة هاته الخوارزمية في ترتيب مجموعة من المعطيات وفق علاقة ترتيب معينة وكم تستهلك من الذاكرة الرئيسية (Mémoire principale) أثناء قيامها بعملية الترتيب، فالمبرمج يريد أن يكون برنامجه سريعاً أكبر ما يمكن ويستهلك أقل ما يمكن من ذاكرة الحاسوب وبالتالي فإذا كان مطالب بترتيب معطيات ما فيجب عليه إختيار الخوارزمية الأفضل التي تتميز بهاته الخواص.
سنتحدث بعض الشيء عن قياس سرعة الخوارزميات ولن نغوص في التفاصيل، لأن قياس سرعة الخوارزميات له موضوع وحده بحد ذاته ويحتاج دراسة أكبر وتركيز أكبر وطبعاً إتقان للرياضيات.
ربما قد تبدو المصطلحات غريبة بعض الشيء، وذلك لأن كل شيء في الإعلام الآلي بالإنجليزية ولم أجد مرادفات بالعربية تصف بدقة ما سنتحدث عنه، لكني سأضع المرادف باللغة الفرنسية ربما سيقرب المعنى :/
التعقيد الزمني (Complexité temporelle) : ويقصد به الزمن الذي تستغرقه الخوارزمية لترتيب مجموعة من البيانات وتنظيمها وفق علاقة ترتيب معينة، ويمكن قياسها بعدد المقارنات التي تقوم بها الخوارزمية أثناء قيامها بعملية الترتيب (في مثالنا السابق تقاس سرعة خوارزمية الترتيب بعدد المقارنات بين الأعداد في الجدول أي كم قارنا من مرة عدد وعدد آخر حتى تمكنا من معرفة العدد الأكبر والعدد الأصغر حتى يتسنى لنا ترتيب هذا الجدول)
يمكن التحدث عن هذا التعقيد الزمني (Complexité temporelle) في عدة حالات نذكر منها : التعقيد الزمني المتوسط (وهو الزمن المستغرق في ترتيب مجموعة من المعطيات في الحالة العادية)، التعقيد الزمني في أسوء الحالات (وهو الزمن المستغرق الأعظم لترتيب مجموعة من المعطيات بحيث أن خوازمية الترتيب التي سنستعملها لن تستغرق زمناً أكبر من هذا الزمن في أسوء الحالات )
التعقيد الفضائي (Complexité spatiale) : ويقصد به الفضاء المستهلك من الذاكرة (Mémoire principale) أثناء القيام بترتيب هاته المعطيات : كم تستهلك الخوارزمية من حجم الذاكرة لترتيب مجموعة من البيانات ؟ فنحن نعلم أن أغلب التعليمات التي نكتبها في برامجنا بعد ترجمتها إلى لغة الآلة (Code machine) أو يمكن القول كود ثنائي (Code binaire) وبعد تشغيلها فهي تشحن في الذاكرة الرئيسية (Mémoire principale) حتى يتسنى للمعالج تطبيق هاته التعليمات تعليمة وراء تعليمة من كل تعليمات البرنامج الذي كتبناه، هذه التعليمات تتعامل بدورها مع الذاكرة فنجد أنه يتم تعريف متغيرات ساكنة (Declaration de variables statiques) وهي المتغيرات التي نعرفها (Int,Char,Float,Double...) أو تعريف متغيرات من نوع آخر وهي متغيرات ديناميكية (Declaration de variables dynamiques) أو ما يسمى بالمؤشرات (Les pointeurs) وهنا يتم حجز فضاء في الذاكرة في طور إشتغال البرنامج..
ويتعلق هذا الفضاء المستهلك بطبيعة خوارزمية الترتيب بحد ذاتها بدرجة أولى وطريقة ترتيبها للمعطيات، ثم بحجم البيانات المطلوب ترتيبها فكلما كان حجم هاته البيانات كبيراً كان الفضاء المستهلك في الذاكرة أكبر حتى يتسنى للبرنامج ترتيب هاته المعطيات و هذا الفضاء المشغول أو المستهلك يختلف من خوارزمية إلى أخرى ولهذا يمكننا الحكم عن خوارزميات الترتيب وإختيار الأفضل بينها.
كيف يمكن قياس سرعة خوارزميات الترتيب ؟
قياس هاته التعقيدات يتطلب وسائل رياضية وبراهين كذلك، لن نتطرق إليها في هذا الموضوع ويمكن للقارء أن يبحث عنها في الأنترنت . وسنكتفي بذكر النتيجة المتوصل إليها فيما يخص قياس سرعة الخوارزمية والفضاء التي تستهلكه أثناء معالجتها للبيانات المعطاة إليها والمطلوب منها ترتيبها.
يرمز للتعقيد الزمني (أي سرعة الخوارزمية) بالرمز T ويكتب بدلالة عدد المعطيات المراد ترتيبها وتنظيمها وفق علاقة ترتيب معينة، هذا العدد من المعطيات نرمز له بالرمز n ، إذا لدينا الآن رمزين هما T ويقصد به سرعة الخوارزمية والرمز n ويقصد به عدد المعطيات المراد ترتيبها، مثال يمكننا كتابة سرعة خوارزمية ترتيب تسمى الترتيب بالفقاعات (Tri à bulles) كما يلي :
T(n) = O(n²)
نلاحظ أن خوارزمية الترتيب بالفقاعات تقوم بـ n² خطوة(مقارنة) حتى تقوم بترتيب n معطيات (فكما ذكرنا سابقا n يمثل عدد المعطيات المراد ترتيبها)
هناك بعض الخوارزميات التي تستهلك أقضل من ذلك في الحالات المتوسطة مثل خوارزمية الترتيب بالدمج (Tri fusion) حيث تكتب عبارة التعقيد الزمني كالتالي :
T(n) = O(nLog(n))
نلاحظ انه في هذه الحالة يمكننا القول أن خوارزمية الترتيب بالدمج تستهلك زمن أقل من خوارزمية الترتيب بالفقاعات لأن :
nLog(n) < n²
الـ O في هذه الحالة هو ترميز خاص يعرفه الرياضيين بترميز لاندو وقد تم إعتماد هذا الترميز في قياس سرعة الخوارزميات لأن هاته العبارات التي وصلنا إليها ماهي إلا تقريبات لما يؤول الـ n (عدد المعطيات المراد ترتيبها) إلى مالانهاية (L'infini)
وبالتالي نحن كمبرمجين لن يهمنا كثيراً البرهان على هاته العبارات و كيف تم إستنتاجها والوصول إليها بل نريد معرفة الخوارزمية الأفضل من بين خوارزميات الترتيب التي سنراها فيما بعد ، وأما من يريد التعمق في هذا المجال وهو قياس سرعة الخوارزميات فعليه بالبحث أكثر في الأنترنت لأنه لن يتم التطرق لها في هذا الموضوع، ببساطة لأنه كما ذكرت سنستعمل هاته العبارات والترميزات للمقارنة بين خوارزميات الترتيب فقط (ولسبب آخر أني لم أتعمق في هذا المجال كثيراً  )
)
ما هي أهم خوارزميات الترتيب ؟
لقد أدى بروز مشكل ترتيب المعطيات في قيام العديد من المبرمجين والرياضييين بالبحث عن أفضل الخوارزميات التي تقوم بترتيب المعطيات وفق علاقة ترتيب معينة في أقصر مدة زمنية ممكنة (أي تكون أسرع ما يمكن) وبالمقابل لا تستهلك كثيراً من فضاء الذاكرة (أي تستهلك أقل ما يمكن من الذاكرة الرئيسية) فظهرت عدة خوارزميات منذ القرن العشرين ربما فاقت العشرين خوارزمية كلها تقوم بترتيب المعطيات أي كلها لها نفس النتيجة (تقريباً، حيث أننا سنرى فيما بعد أنه يوجد عوامل أخرى للحكم على الخوارزميات لكنها أقل أهمية من سرعة الخوارزمية وإستهلاكها للموارد) لكن هذه الخوارزميات التي تم إيجادها تختلف فيما بينها فيما سبق ذكره.
هناك خوارزميات ترتيب بيداغوجية أي تعليمية فهي تطرح في الجامعات وفي المدارس الخاصة بتعليم البرمجة والخوارزميات وذلك لسهولة فهمها وتطبيقها وبساطتها وإمكانية محاكاتها في الواقع وإمكانية القيام بها يدوياً حتى يستطيع الطالب فهمها، ولكن هذه الأخيرة يقل إستخدامها في الميدان وفي البرامج التي يتم تطويرها لأنه بكل بساطة يوجد ما هو أفضل من هذه الخوارزميات وأسرع منها ويستهلك فضاء ذاكرة أقل منها ويعطي نفس النتيجة وهي ترتيب البيانات.
وجدت جدولاً في ويكيبيديا يجمع حوالي 14 خوارزمية ترتيب مختلفة شامل في تفاصيله قمت بنسخه وترجمته لأنه موجود في ويكيبيديا باللغة الفرنسية
الجدول كاملاً موجود في ويكيبيديا سأضع رابط المقال في آخر الموضوع .. ^^
| الإسم | ت.زمني في أفضل الحالات | ت.زمني في الحالات المتوسطة | ت.زمني في أسوء الحالات | التعقيد الفضائي | الثبات |
| الترتيب السريع |  |  |  | 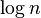 في المتوسط، في المتوسط،  في أسوء الحالات في أسوء الحالات | لا |
| الترتيب بالدمج |  |  |  |  | نعم |
| الترتيب بالإدراج |  |  |  | 1 | نعم |
| الترتيب بالإختيار |  |  |  | 1 | لا |
| الترتيب بالفقاعات |  |  |  | 1 | نعم |
| الترتيب الشجري |  |  |  |  | نعم |
| الترتيب العذب |  |  |  | 1 | لا |
| الترتيب الفردي-الزوجي |  |  |  | 1 | نعم |
هذه بضع خوارزميات فقط من كل خوارزميات الترتيب الموجودة في مجال البرمجة وللأسف لن نتطرق إلى كل هاته الخوارزميات لسبب واضح وهو أن كل خوارزمية من هاته الخوارزميات تتطلب بالإضافة إلى شرح وأمثلة وكود، فيديو يبين كيفية إشتغال هاته الخوارزميات وكيف تقوم بترتيب مجموعة من المعطيات وفق علاقة ترتيب معينة وهذا لأن بعض الخوارزميات لن يكفي كتابة فقرة تشرحها وإعطاء أمثلة عنها حتى يتم فهمها لسبب أنها معقدة بعض الشيء وتتطلب محاكاة بسيطة لها في فيديو أو في عدة صور.
وسنكتفي بهذا القدر في هذا الموضوع، وسأحاول في موضوع آخر مواصلة ما بدأته في هذا الموضوع وسنتطرأ إلى عوامل أخرى للحكم عن خوارزميات الترتيب والتفريق بينها لكن هذه العوامل تقل أهمية عن السرعة والفضاء المستهلك، لكنها في بعض الأحيان تكون مهمة ويجب الإنتباه إليها على حسب المطلوب في البرنامج الذي نقوم بتطويره، هذه العوامل هي : خاصية الترتيب الثابت وخاصية الترتيب الآني أو ما يسمى بالترتيب المكاني (وهي الخوارزميات التي نقوم بترتيب مجموعة من المعطيات في نفس البنية التي أدخلت إليها ولا تلجئ إلى فضاء آخر ومتغيرات جديدة لتقوم بالترتيبها). وسنحاول التطرأ إلى بعض هاته الخوارزميات كشرح وتطبيق وأمثلة إن شاء الله.
ليست هناك تعليقات: